Система упражнений по теме «Тригонометрические уравнения»
б) ![]() ; г)
; г) ![]() .
.
№5. Решите уравнение:
а) ![]() ; б)
; б) ![]() .
.
№6. Решите уравнение:
а) ![]() ; б)
; б) ![]() .
.
№7. Решите уравнение:
а) ![]() ; б)
; б) ![]() .
.
№8. Решите уравнение:
а) ![]() ; б)
; б) ![]() .
.
№9. Решите уравнение:
а) ![]() ; б)
; б) ![]() .
.
Методические рекомендации.
Как уже было замечено ранее, упражнения, представленные на этом уроке, позволяют ученику понять связь между решением тригонометрического уравнения и квадратного уравнения. Нетрудно также видеть, что решение тригонометрического уравнения, в конечном счете, сводится к решению простейшего тригонометрического уравнения, т.е. реализуется принцип дидактической спирали – непрерывного изучения материала всего школьного курса в контексте новой темы.
Задания, представленные под номерами 1 – 4, являются обязательными заданиями, их должен уметь решать каждый учащийся. Задания №5 - №9 рассчитаны на ученика, претендующего на оценку «4» и более.
Урок №9
После того, как учащиеся научились решать тригонометрические уравнения с помощью введения новой переменной, а также научились решать тригонометрические уравнения, сводимые к квадратным уравнениям, следует перейти к решению уравнений с помощью разложения на множители.
№1. Решите уравнение:
а) 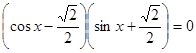 ;
;
б) ![]()
№2. Решите уравнение:
а) ![]() ; б)
; б) ![]() .
.
№3. Решите уравнение:
а) ![]() ; б)
; б) ![]() .
.
№4. Решите уравнение:
а) ![]() ;
;
б) ![]() .
.
№5. Решите уравнение:
а) ![]() ; б)
; б) ![]() .
.
№6. Решите уравнение:
а) ![]() ; б)
; б) ![]() .
.
№7. Решите уравнение:
а) ![]() ; б)
; б) ![]() .
.
№8. Решите уравнение:
а) ![]() ;
;
б) ![]() .
.
№9. Решите уравнение:
а) ![]() ;
;
б) ![]() .
.
Методические рекомендации.
Большое внимание следует здесь уделить заданиям, представленным под номерами 5, 6. При решении задания №5 следует обратить внимание учащихся на возможное появление постороннего корня, и поэтому следует четко отслеживать область допустимых значений выражения, стоящего в правой части нашего уравнения. Аналогичное замечание справедливо и для №6.
Рассмотрим решение п. б) из №8.
№8. Решить уравнение.
б) ![]() .
.
Решение
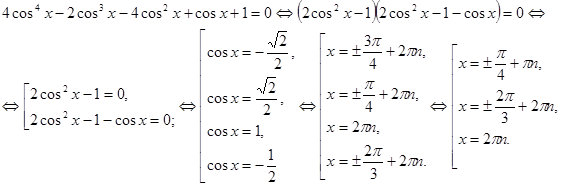
Задачи речевого развития в старшей группе детского
сада
В программе воспитания и обучения в детском саду под редакцией А.М. Васильевой говорится о следующих задачах речевого развития детей в старшей группе детского сада.
Развивающая речевая среда
Продолжать развивать речь как средство общения. Расширять представления детей о многообразии окружающего ...
Виды внимания
Наиболее простым видом внимания является непроизвольное.
Непроизвольным называют такой вид внимания, который возникает у человека без сознательно поставленной цели и волевого усилия. Часто такое внимание выступает в единстве с ориентировочным рефлексом. Ученик уронил книгу, с громким стуком она у ...
Свойства внимания
Объем внимания определяется числом объектов, которые может быть охвачено вниманием в момент времени. Если ученику показать таблицу, на которой нарисован ряд предметов (независимо друг от друга), то в момент времени (1–2 секунды), он заметит несколько нарисованных предметов, что определит объем его ...
Главные разделы
- Главная
- Методы обучения двигательным действиям
- Раннее обучение английскому языку
- Педагогика способностей
- Половое воспитание детей и подростков
- Я-концепция ребенка дошкольного возраста
- Коррекция гиперактивных детей
- Информация о педагогике
