Система упражнений по теме «Тригонометрические уравнения»

№1. Решите уравнение:

а) ; б)

№2. Решите уравнение:

а) ; б) .

№3. Решите уравнение:

а) ; б) .

№4. Решите уравнение:

а) ; б) .

№5. Решите уравнение:

а) ; б) .

№6. Решите уравнение:

а) ; б) .

№7. Решите уравнение:

а) ;

б) .

№8. Сколько корней имеет уравнение:

а) , на отрезке ;

б) , на отрезке ?

№9. Докажите тождество:

а) 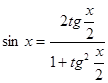; б) .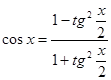

№10. Используя замену и тождества из упражнения №9, решите уравнения:

а) ; б) .

№11. Решите уравнение:

а) ;

б) .

№12. Решите уравнение:

а) ;

б) .

Методические рекомендации.

Как уже было сказано выше, при последовательном переходе от одного упражнения к другому их сложность увеличивается. В чем это проявляется? В первых двух заданиях от учащихся требуется простое применение формулы двойного аргумента, при помощи которой уравнение сводится к простейшему тригонометрическому уравнению. Задания №3 - №5 приводят исходное уравнение к квадратному, а потом, уже после решения соответствующего квадратного уравнения, мы приходим к решению простейшего тригонометрического уравнения. Т.е. здесь нам требуется выполнить больше преобразований.

Продолжая последовательное передвижение от номера к номеру, отчетливо видно, что количество преобразований увеличивается.

В задании №11 до сознания ученика доводится тот факт, что аргументом тригонометрической функции может являться многочлен второй более высоких степеней.

Приведем решение уравнения из №11 и п. а) №12.

№11. Решить уравнение:

а) .

Решение

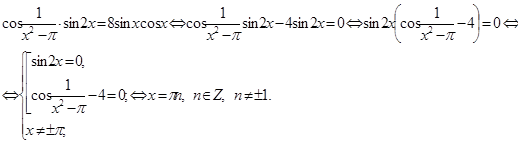
№12. Решить уравнение:

а) .

Решение

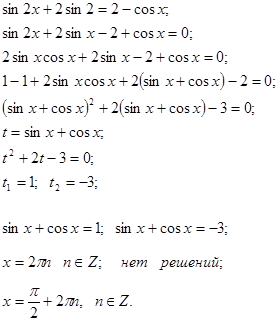
Аналогичным образом решается и п. б).

Урок №10

Тема урока: Формулы понижения степени».

№1. Решите уравнение:

а) ; б) .

№2. Решите уравнение:

а) ; б) .

№3. Решите уравнение:

Главные разделы

• Главная
• Методы обучения двигательным действиям
• Раннее обучение английскому языку
• Педагогика способностей
• Половое воспитание детей и подростков
• Я-концепция ребенка дошкольного возраста
• Коррекция гиперактивных детей
• Информация о педагогике