Система упражнений по теме «Тригонометрические уравнения»
Приведем решение уравнений из №3.
№3. Найдите корни уравнения на заданном промежутке:
а)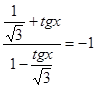 
, 
.
Решение
.
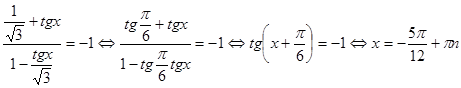Осуществляя перебор по параметру n, получаем корни уравнения на заданном промежутке.
Ответ: 
б)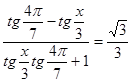 
, 
.
Решение
.
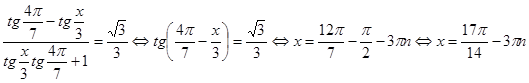После перебора корней получаем ответ.
Ответ: 
.
Урок №7
Контрольная работа по материалам уроков №1 – №6.
Вариант 1
№1. Найдите значения выражений:
а) 
;
б) 
.
№2. Упростите выражения:
а) 
б) 
.
№3. Докажите тождество
.
№4. Решите уравнение
.
№5. Зная, что 
, найдите 
.
№6. Известно, что 
.
Найдите 
.
Вариант 2
№1. Найдите значения выражений:
а) 
;
б) 
.
№2. Упростите выражения:
а) 
;
б) 
.
№3. Докажите тождество
.
№4. Решите уравнение
.
№5. Зная, что 
, найдите 
.
№6. Известно, что 
.
Найдите 
.
Методические рекомендации.
Контрольная работа представлена по материалам уроков №1 – №6.
Цель контрольной работы – проверить сформированность умения выполнять тождественные преобразования тригонометрических выражений, используя формулы синуса и косинуса суммы и разности аргументов, а также умения применять изученные преобразования при решении тригонометрических уравнений.
В предложенной контрольной работе не были представлены задания, связанные с преобразованием выражений, содержащих тангенс суммы или разности аргументов. Формула тангенса суммы или разности аргументов отчетливо вытекает из формул косинуса и синуса суммы или разности аргументов, а также из определения тангенса.
Обязательному уровню усвоения учебного материала здесь соответствуют задания, представленные под номерами 1 – 4.
Пятое задание является заданием среднего уровня сложности, а шестое повышенного уровня сложности.
За выполнение заданий базового уровня ставится оценка «3». В случае успешного выполнения заданий базового уровня и одного из заданий более высоких уровней, ставится оценка «4», за выполнение всех заданий – оценка «5».
Урок №8 – №9
Тема урока: «Формулы двойного аргумента».
При изложении материала данных двух уроков мы будем придерживаться той схемы, которая была предложена в предыдущих уроках.
Однако при разработке системы упражнений следует учитывать тот факт, что при последовательном переходе от одного упражнения к другому, постепенно увеличивается их сложность. Кроме заданий на простое применение формул двойного аргумента, появляются задания, в которых данный материал комбинируется с материалом предыдущих уроков, в том числе и с материалом §1.
Использование различных форм и видов проверки знаний учащихся в начальных
классах на уроках окружающего мира
Рассмотрим подробнее способы контроля знаний на уроке «Окружающий мир».
При текущем и наиболее частом виде контроля используются индивидуальный и фронтальный опрос, который может быть как устным, так и письменным.
Устный опрос – это диалог учителя с одним учеником (индивидуальный опрос) или со в ...
Формы, методы и средства обучения творческим работам с
использованием информационных технологий
В данном параграфе представлены формы, методы и средства обучения работам с графическими редакторами.
Формы обучения
Формы организации обучения представляют собой внешнее выражение согласованной деятельности учителя и учеников, осуществляемой в установленном порядке и определенном режиме. В рамк ...
Современное состояние
берестяного промысла
Приятно осознавать, что в настоящее время берестяной промысел не угас.
“Берестяные" - центры России - это Великий Устюг, Вологда, Русский Север, Киров, Урал, Новгород, Архангельск, Томск, Новосибирск, Ярославль и некоторые другие города, где растет береза.
В различных регионах в процессе об ...
Главные разделы
- Главная
- Методы обучения двигательным действиям
- Раннее обучение английскому языку
- Педагогика способностей
- Половое воспитание детей и подростков
- Я-концепция ребенка дошкольного возраста
- Коррекция гиперактивных детей
- Информация о педагогике