Система упражнений по теме «Тригонометрические уравнения»
Задания №1 - №6 являются обязательными для всех учащихся.
Как можно было заметить ранее, система упражнений, представленная к урокам №1 - №7 (в дальнейшем это будет справедливо при подборе упражнений и на последующих уроках), составлена таким образом, чтобы показать учащимся связь между преобразованиями, которые они изучали с 7 по 9 касс, и тригонометрическими уравнениями. Сначала от учащихся требуется простое понимание того, что тригонометрические функции могут принимать как положительные, так и отрицательные значения. Затем до сознания учеников доводиться тот факт, что любое тригонометрическое уравнение сводится к простейшему при помощи несложных преобразований, которые они уже знают (разложение на множители, введение новой переменной 
, приведение к квадратному уравнению).
Приведем решение № 9 (п. (а)) и №12.
№9. Найти корни заданного уравнения на заданном промежутке:
а) 
.
Решение
Однако для решения нашего уравнения данная запись формулы для нахождения корней тригонометрического уравнения не является удобной, поэтому воспользуемся другой записью
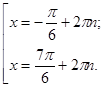
Нетрудно видеть, что простым перебором по параметру n мы сразу получаем все требуемые корни уравнения, т.е.:
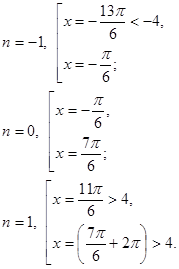
Ответ: 
.
№12. Решить уравнение:
а) 
.
Решение
В данном уравнении речь идет об отыскании корней уравнения 
на отрезке 
. Из серии 
этому отрезку принадлежат только три значения: 
.
Однако 
и 
также являются решением данного уравнения, поэтому ответом будут являться следующие значения: 
.
б) 
.
Решение
Так же как и в п. а), рассмотрим серию решений уравнения 
, накладывая на нее следующие ограничения: 
.
Серией решения уравнения являются следующие значения x: 
.
Очевидно, что неравенствам не будет удовлетворять только значение 
(при 
).
Ответ: 
.
Урок №8
На данном уроке целесообразно рассмотреть еще один случай введения новой переменной при решении тригонометрических уравнений: решение тригонометрических уравнений, сводящихся к квадратным уравнениям.
№1. Решите уравнение:
а) 
; б) 
.
№2. Решите уравнение:
а) 
; б) 
.
№3. Решите уравнение:
а) 
; б) 
.
№4. Решите уравнение:
а) 
; в) 
;
Природа и духовное начало народных воспитательных
традиций, преемственность поколений
Духовность нации - сложное понятие. В русской религиозной философии оно использовалось прежде всего для объяснения самостоятельности культурной субстанции народа и определяющей роли исторических судеб наций. В советской теории оно не было столь употребимо и не нашло своего места как в системе по ...
Теоретические основы реализации коммуникативного метода обучения
иностранным языкам
Метод - это система функционально взаимообусловленных частнометодическнх принципов, объединенная единой стратегической идеей, направленной на обучение какому-либо виду речевой деятельности. Для коммуникативного метода такой идеей является коммуникативность обучения. Следовательно, построение проце ...
Понятие «аутентичность» в методике
Существуют различные подходы к описанию всех аспектов аутентичности. Остановимся на некоторых из этих подходов.
X. Уиддоусон рассматривает аутентичность не столько как свойство, присущее речевому произведению, сколько как характеристику учебного процесса. Он разграничивает понятия «подлинность» и ...
Главные разделы
- Главная
- Методы обучения двигательным действиям
- Раннее обучение английскому языку
- Педагогика способностей
- Половое воспитание детей и подростков
- Я-концепция ребенка дошкольного возраста
- Коррекция гиперактивных детей
- Информация о педагогике