Система упражнений по теме «Тригонометрические уравнения»

№2. Решите уравнение:

а) ; б).

№4. Решите уравнение:

а) ; б) .

№5. Решите уравнение:

а) ; б) .

№6. Решите уравнение:

а) ; в) ;

б) ; г) .

№7. Решите уравнение:

а) ; б) .

Урок №3 – №4

Тема урока: «Синус и косинус разности аргументов».

Так же, как и в случае синуса и косинуса суммы аргументов, на первом уроке целесообразно дать учащимся вывод формул и отработать с ними доказательства тождеств, тригонометрические преобразования, а на втором уроке – следует начать с учащимися решать тригонометрические уравнения, имеющие прямое отношение к данной теме. Такое построение учебного материала показывает связь между решением тригонометрических уравнений и тригонометрическими преобразованиями.

№1. Решите уравнение:

а) ;

б) .

№2. Решите уравнение:

а) ; б) .

№3. Решите уравнение:

а) ; б) .

№4. Решите уравнение:

а) ;

б) .

№5. Решите уравнение:

а) ;

б) .

№6. Решите уравнение:

а) ; б) .

№7. Решите уравнение:

а) ; б) .

Урок №5 – №6

Тема урока: «Тангенс суммы и разности аргументов».

При проведении этих уроков желательно придерживаться схемы изложения материала, которая представлена для уроков №1 - №4, т.к. такое изложение материала способствует осознанию учащимися связи между тригонометрическими преобразованиями и тригонометрическими уравнениями и открывает перед учащимися смысл изучаемых тригонометрических преобразований.

№1. Решите уравнение:

а) ; б) .

№2. Решите уравнение:

а) 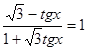; в) .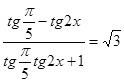

№3. Найдите корни уравнения на заданном промежутке:

а) , ;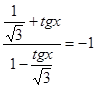

б) , .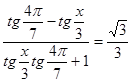

№4. Решите неравенство:

а) 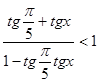; б) .

Методические рекомендации.

Задание №4 не является обязательным для решения всеми учащимися, однако, оно дает нам возможность лишний раз обратиться к числовой окружности. Более того, решая данные неравенства, мы опять приходим к решению простейшего тригонометрического уравнения.

Главные разделы

• Главная
• Методы обучения двигательным действиям
• Раннее обучение английскому языку
• Педагогика способностей
• Половое воспитание детей и подростков
• Я-концепция ребенка дошкольного возраста
• Коррекция гиперактивных детей
• Информация о педагогике