Система упражнений по теме «Тригонометрические уравнения»

Решение тригонометрических уравнений с помощью введения новой переменной .

Решение тригонометрических уравнений, приводимых к квадратным уравнениям.

Решение тригонометрических уравнений с помощью разложения на множители.

Решение однородных тригонометрических уравнений и уравнений, приводимых к ним.

тригонометрический уравнение урок методический

Урок №7

№1. Решите уравнение:

а) ; б) .

№2. Решите уравнение:

а) ; б) .

№3. Решите уравнение:

а) ; б) .

№4. Решите уравнение:

а) ; б) ;

б) ; г) .

№5. Решите уравнение:

а) ; б) .

№6. Решите уравнение:

а) ; в) .

№7. а) Найдите корни уравнения , принадлежащие отрезку .

б) Найдите корни уравнения , принадлежащие отрезку .

№8. Найдите корни заданного уравнения на заданном промежутке:

а) ; в) ;

б) ; г) .

№9. Найдите корни заданного уравнения на заданном промежутке:

а) ; в) ;

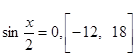б) ; г) .

№10. Решите уравнение и найдите:

а) наименьший положительный корень;

б) корни, принадлежащие отрезку .

№11. Решите уравнение и найдите:

а) наибольший отрицательный корень;

б) корни, принадлежащие интервалу .

№12. Решите уравнение:

а) ; в) ;

б) ; г) .

Методические рекомендации.

Задания, представленные под номерами 9 – 11, не являются обязательными, однако, именно эти номера (т.к. здесь мы имеем место с отбором корней тригонометрического уравнения) позволяют учащимся осознать роль параметра в формуле корней тригонометрического уравнения.

Задания, аналогичные №12, можно также решать с учащимися и при решении тригонометрических уравнений с помощью разложения на множители, но, т.к. при решении уравнений данного типа (область допустимых значений здесь не вся числовая прямая, т.е. имеют место некоторые ограничения) также можно говорить об отборе корней тригонометрического уравнения.

Главные разделы

• Главная
• Методы обучения двигательным действиям
• Раннее обучение английскому языку
• Педагогика способностей
• Половое воспитание детей и подростков
• Я-концепция ребенка дошкольного возраста
• Коррекция гиперактивных детей
• Информация о педагогике