Фрагмент урока для 11-го класса по теме «Иррациональные уравнения»
Комментарии к уроку
Тип данного урока - введение нового материала. Его основная цель - ввести понятие иррациональных уравнений и развивать умение применять способы решения иррациональных уравнений. Урок разработан таким образом, что учащиеся, путем исследования, самостоятельно выводят алгоритм решения иррациональных уравнений и ее свойства. На уроке используются такие приемы коллективной формы обучения, как решение проблемно-поисковых задач и самостоятельное проведение исследования.
Оборудование: плакаты; карточки.
Изложение нового материала – 13 мин.
На магнитной доске висят карточки с уравнениями.
Учитель: Прошу вашего внимания на доску. Здесь расположены карточки, на которых записаны уравнения. Посмотрите внимательно и определите, какие уравнения вы уже умеете решать, а какие у вас вызывают затруднения?
Карточки:
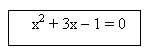
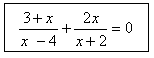
Кто из вас может выйти к доске убрать карточки с уравнениями, которые вы можете решить и назвать их тип?
Вывод: Остались карточки с уравнениями, которые вы еще не умеете решать.
Чем отличается запись этих уравнений от тех, которые мы убрали?
(Предполагаемый ответ: неизвестное находится под знаком корня).
Верно! Такие уравнения, в которых под знаком корня содержится переменная, называются иррациональными уравнениями.
Итак, построим алгоритм решения простейших иррациональных уравнений, рассмотрим некоторые способы решения более сложных иррациональных уравнений.
Учитель объясняет алгоритм решения и оформления иррациональных уравнений.
Берет первую карточку с уравнением, прикрепляет к основной доске и решает его.
Решение.
Основной метод решения иррациональных уравнений – это метод возведения в квадрат обеих частей уравнения. Но при этом мы можем получить неравносильное уравнение, поэтому в конце обязательно нужно сделать проверку.
Возведем обе части уравнения в квадрат, получим
Проверка.
При 
верное равенство.
При 
верное равенство.
3. Следовательно, числа –3 и 3 являются решениями данного иррационального уравнения.
Ответ: -3; 3.
Учитель: А как бы вы решали вот такое уравнение: 
.
2. Выходит учащийся к доске и решает второе уравнение этим же способом.
Решение.
Возведем обе части уравнения в квадрат, получим 
Проверим, являются ли полученные значения переменной решениями данного уравнения?
Проверка.
При 
верное равенство.
При 
верное равенство.
Следовательно, число 2 является решением данного уравнения.
(Ответ: 2).
Итак, получили, что только одно значение переменной является решением данного уравнения. Это число 2. Число –1 в данном случае называется посторонним конем.
Вопрос к отвечающему: «Скажи, важна ли проверка в иррациональных уравнениях, решаемых таким способом и почему?»
(Предполагаемый ответ: да, так как могут появиться посторонние корни).
Учитель: Возможность появления посторонних корней обязывает нас быть очень внимательными при решении иррациональных уравнений.
Психология полового воспитания на различных возрастных этапах
Эффективность полового воспитания зависит от учета связанных с полом особенностей развития ребенка на всех возрастных этапах, начиная с самых ранних. В первые годы жизни особое значение имеет дифференцированное отношение к ребенку родителей, т.е. обращение с ним именно как с мальчиком или девочкой ...
Сущность понятия «формулы речевого этикета»
Речь – явление социальное и служит средством общения людей друг с другом. Своевременное и правильное речевое развитие - необходимое условие формирования личности ребенка. В процессе развития речи ребенок овладевает языком. Усвоение речи в дошкольном возрасте – необходимое условие для овладения гра ...
Особенности Я-концепции у детей дошкольного возраста
Каждый человек стремится к одобрению со стороны других людей. В раннем и дошкольном детстве такой значимой группой выступают члены семьи. Важно, чтобы они относились к ребенку как к достойному существу, способному к определенным видам деятельности, что в свою очередь формирует в нем чувство собств ...
Главные разделы
- Главная
- Методы обучения двигательным действиям
- Раннее обучение английскому языку
- Педагогика способностей
- Половое воспитание детей и подростков
- Я-концепция ребенка дошкольного возраста
- Коррекция гиперактивных детей
- Информация о педагогике