Система упражнений по теме «Тригонометрические уравнения»
Урок №4
Тема урока: «Арксинус и решение уравнения ![]() ».
».
№1. Вычислите:
а) ![]() ; в)
; в) ![]() ;
;
б) ![]() ; г)
; г) ![]() .
.
№2. Вычислите:
а) 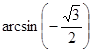 ; в)
; в) ![]() ;
;
б) ![]() ; г)
; г) 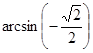 .
.
№3. Вычислите:
а) ![]() ; в)
; в) 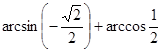 ;
;
б) ![]() ; г)
; г) ![]() .
.
№4. Вычислите:
а) ![]() ; в)
; в) 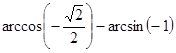 ;
;
б) 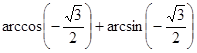 ; г)
; г) 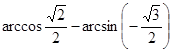 .
.
№5. Докажите тождество:
а) ![]() ;
;
б) ![]() .
.
№6. Вычислите:
а) ![]() ;
;
б) 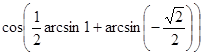 ;
;
в) 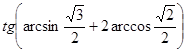 ;
;
г) 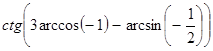 .
.
№7. Найдите область допустимых значений выражения:
а) ![]() ; в)
; в) ![]() ;
;
б) ![]() ; г)
; г) ![]() .
.
№8. Имеет ли смысл выражение:
а) ![]() ; в)
; в) ![]() ;
;
б) ![]() ; г)
; г) ![]() .
.
№9. Вычислите:
а) ![]() ; в)
; в) ![]() ;
;
б) ![]() ; г)
; г) ![]() .
.
Методические рекомендации.
При отборе задач необходимо показать учащимся связь с понятием арккосинуса, которое было изучено ранее, поэтому в системе упражнений необходимо давать новое понятие арксинуса в комбинации с уже изученным ранее понятием и его свойствами.
Задания под номером 6 – 9 рассчитаны на учащихся, претендующих на оценку, отличную от оценки «3».
Урок №5
Тема урока: «Арксинус и решение тригонометрического уравнения ![]() »
»
№1. Решите уравнение:
а) ![]() ; в)
; в) ![]() ;
;
б) ![]() ; г)
; г) ![]() .
.
№2. Решите уравнение:
а) ![]() ; в)
; в) ![]() ;
;
б) ![]() ; г)
; г) ![]() .
.
№3. Решите уравнение:
а) ![]() ; в)
; в) ![]() ;
;
б) ![]() ; г)
; г) ![]() .
.
Умственное воспитание
Умственное воспитание ребенка рассматривается не только как овладение им знаниями и способами мыслительной деятельности, но и как формирование определенных качеств личности.
Умственное воспитание детей происходит как в ходе общения со взрослыми, в играх со сверстниками, так и в процессе системати ...
Методика оценки эффективности применения информационных ресурсов в учебном
процессе
Разработка и эксплуатация информационных образовательных ресурсов неразрывно связана с оценкой эффективности их применения в образовательном процессе. Образовательная среда как педагогическая система, в которой реализуется учебно-воспитательный процесс, в общем случае состоит из таких элементов, к ...
Методы, принципы, факторы и условия, активизирующие педагогическое
воздействие учителя начальных классов
Для того чтобы осуществлять многогранную задачу воспитания, вовлекать детей в целесообразную деятельность и систему отношений, необходим богатый арсенал средств и методов педагогического воздействия, способных мобилизовать, организовать, активизировать деятельность воспитанников, просветить их соз ...
Главные разделы
- Главная
- Методы обучения двигательным действиям
- Раннее обучение английскому языку
- Педагогика способностей
- Половое воспитание детей и подростков
- Я-концепция ребенка дошкольного возраста
- Коррекция гиперактивных детей
- Информация о педагогике
