Разработка занятий элективного курса

Постановка домашнего задания

Решить уравнения и неравенство:

1) ;

2) ;

3) ;

4) .

Занятие №7 Тема: «Использование неотрицательности функций, входящих в уравнение или неравенство».

Цели: познакомить учащихся с приемом решения уравнений и неравенств, состоящих из неотрицательных функций.

Ход занятия:

Проверка домашнего задания. На доске записывается ответ к каждому заданию. Уравнение, вызвавшее трудности, разбирается учеником, выполнившим его.

Изучение нового материала.

Утверждение 1. Пусть имеется уравнение . Если множество значений каждой из функций принадлежит промежутку , то уравнение равносильно системе .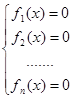

‑Назовите функции, которые принимают неотрицательные значения на всей области определения ().

Пример1. Решить уравнение .

Преобразуем уравнение . Наше уравнение будет равносильно системе 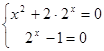, которая не имеет решений. Значит и исходное уравнение решений не имеет.

Аналогичное утверждение можно сформулировать и для неравенств.

Утверждение 2. Пусть имеется неравенство . Если множество значений каждой из функций принадлежит промежутку , то неравенство равносильно системе .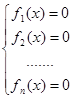

Пример 2. Решить неравенство .

Так как для любого x справедливы неравенства , то неравенство равносильно системе 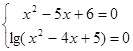, решением которой является . Значит, неравенство имеет единственное решение .

Утверждение 3. Пусть имеется неравенство . Если множество значений каждой из функций принадлежит промежутку , то решениями неравенства являются все x из ОДЗ, за исключением тех x, которые являются решениями системы .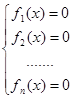

Пример 3. Решить неравенство

ОДЗ неравенства . Для нахождения решения неравенства нужно исключит из его ОДЗ все решения системы . Решениями неравенства являются все x из множества .

Решение задач. На доске написаны два варианта заданий. Учащиеся в течение 13-15 минут решают каждый свой вариант, затем в паре обмениваются тетрадями и проверяют решение соседа по парте и ставят баллы (по одному за каждое верное решение уравнения или неравенства). Учитель выписывает ответы на доске.

Вариант 1.

;

Главные разделы

• Главная
• Методы обучения двигательным действиям
• Раннее обучение английскому языку
• Педагогика способностей
• Половое воспитание детей и подростков
• Я-концепция ребенка дошкольного возраста
• Коррекция гиперактивных детей
• Информация о педагогике