Разработка занятий элективного курса

Решение задач. Список заданий написан на доске. Первое и второе учитель подробно разбирает. Остальные учащиеся самостоятельно решают в тетради и по желанию демонстрируют свое решение на доске.

1) Решить уравнение

Период, входящих в уравнение функций Т=200p. Возведем обе части в квадрат и получим ; . Проверим корни в пределах периода:

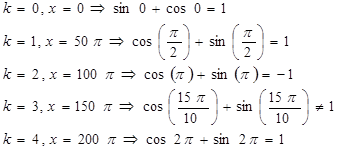
Решением уравнения является .

2) Решить уравнение ;

Заметим, что в обеих частях уравнения стоят четные функции, поэтому решим данное уравнение с использованием свойств четной функции. С учетом сказанного выше для четной функции, достаточно найти решения для x≥0. Но x=0 не есть корень уравнения. Рассмотрим два промежутка (0, 2], (2, ∞). На промежутке (0, 2] имеем ; ; x=. На промежутке (2, ∞) имеем ; ; 3x=2x; x=0. Но так как x=0 не является корнем уравнения, то для x>0 данное уравнение имеет корень x=. Но тогда x= ‑ также является корнем уравнения.

3) ;

4) .

Подведение итогов занятия.

Учитель выставляет баллы учащимся по одному баллу за решение домашнего задания и за решение у доски.

Постановка домашнего задания. На этом занятии завершается теоретическая часть курса. Следующий урок посветим решению разных задач. Поэтому вам нужно повторить всю теорию, посмотреть приемы решения уравнений и неравенств, рассмотренные нами на предыдущих занятиях. Занятие пройдет в форме игры. Класс нужно разделить на команды. Каждая команда готовит название, девиз.

Занятие №9 «Морской бой»

Цели: закрепить имеющиеся знания учащихся по изученному материалу.

Правила игры.

Занятие проводится в форме игры «Морской бой». Основой игры является детская игра «Морской бой». Поле с проставленными на нем очками является игровым полем для данной игры. Например, для морского боя 5*5 клеток игровое поле и поле ведущего будут выглядеть следующим образом:

На игровом поле проставлены очки и буквы «Б» блиц-турнир (за 60 секунд ответить на максимальное количество вопросов), «М» - музыкальный конкурс (спеть песни, в которых содержаться числительные, кто больше), «К» - конкурс капитанов.

На поле у ведущего расположены корабли, координат которых играющие не знают.

Команды распределяют между собой поровну корабли (по 2 корабля каждой команде) и ведущий называет командам в тайне от других координаты этих кораблей.

Та команда, которой выпадает по жребию начинать игру, называет координату первого «выстрела». Если на этой клетке стоит корабль, то команда получает в плюс очки, проставленные на клетке и продолжает стрельбу. Если на этой точке нет корабля, то ведущий предлагает команде вопрос той сложности, сколько очков стоит на этой клетке. Если команда ответила правильно, то очки засчитываются в плюс, если неправильно или не ответила, то в минус. Ход переходит к противнику.

Команда выбывает из игры, если «потоплены» все её корабли. Выигрывает та команда, которая к моменту, когда сбиты все корабли, наберет больше очков (победителем может считаться и та команда, у которой остался последний корабль «на плаву»).

Главные разделы

• Главная
• Методы обучения двигательным действиям
• Раннее обучение английскому языку
• Педагогика способностей
• Половое воспитание детей и подростков
• Я-концепция ребенка дошкольного возраста
• Коррекция гиперактивных детей
• Информация о педагогике