Разработка занятий элективного курса
б) обобщить и систематизировать знания учащихся о монотонности функций, способах исследования функции на монотонность.
Ход занятия:
Проверка домашнего задания. Решение первого задания учитель разбирает устно, ученики проверяют в тетради. Решение 2-ого и 3-его один ученик выписывает на доску до начала занятия. Школьники сверяют со своим решением, учитель комментирует решение.
Изучение нового материала.
Доклад «Способы доказательства возрастания (убывания) функций».
Доклад «Как монотонность помогает решать уравнения и неравенства».
Учитель делает выводы по докладам.
Решение задач. Список задач написан на доске. 1-ое задание разбирается учителем. На остальные дается время для самостоятельного решения. После ученики по желанию показывают свое решение на доске.
Решите уравнение или неравенство:
;
;
;
;
;
;
.
Подведение итогов занятия.
Учитель выставляет баллы за работу на занятии. По одному баллу за доклад, по одному баллу за каждую задачу, решенную у доски.
Постановка домашнего задания.
;
;
.
Занятие №4 Тема: «Уравнения вида 
.»
Цель: систематизировать и обобщить знания о методе решения уравнений вида .
Ход занятия:
Организационный момент. Постановка целей занятия, темы и плана его проведения.
Проверка домашнего задания. Решение каждой задачи с места объясняют ученики. Если нужно, учитель корректирует и комментирует ответы учеников.
Решение задач. Решение первой задачи учитель подробно разбирает на доске.
.
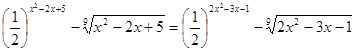В обеих частях уравнения стоят функции, похожие внешне. Поэтому имеет смысл рассмотреть функцию 
.
‑ Назовите область определения этой функции (R).
‑ Исследуйте функцию на монотонность (убывает на R).
Если выполняются эти условия, то исходное уравнение равносильно уравнению 
. Найдем корни этого уравнения, они будут корнями исходного уравнения.
. В этом задании следует обратить внимание учеников на то, что функция 
определена не на всей числовой прямой, поэтому уравнение 
равносильно системе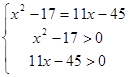 
;
;
;
.
Подведение итогов занятия.
Учащимся, решившим верно все задания, за урок ставится 3 балла.
Постановка домашнего задания.
Повторить теоретический материал, связанный с понятием области изменения функции.
Решить уравнения:
;
;
;
Математические задачи, решаемые при помощи движений
Существенным элементом структуры познавательного педагогического процесса являются методы обучения. Под методом обучения будем понимать упорядоченный способ взаимосвязанной деятельности учителя и учащихся, направленный на достижение целей обучения. Система методов обучения состоит из общих методов ...
Построение и методика проведения занятий. Особенности руководства ими
Решающим условием обучения является рациональность избираемой методики, которая строится на основе учета возрастных особенностей детей и их физической подготовленности. При этом в полной мере необходимо учитывать интересы и возможности детей.
Процесс обучения двигательным действиям можно условно ...
Классификация понятий
Классификация – распределение предметов по группам (классам), при котором каждый класс имеет свое постоянное место.
Классификация является разновидностью деления понятия, представляет собой вид последовательного деления и образует развернутую систему, в которой каждый ее член (вид) делится на под ...
Главные разделы
- Главная
- Методы обучения двигательным действиям
- Раннее обучение английскому языку
- Педагогика способностей
- Половое воспитание детей и подростков
- Я-концепция ребенка дошкольного возраста
- Коррекция гиперактивных детей
- Информация о педагогике