Разработка занятий элективного курса

Рассмотрим на примере, как при решении уравнений знание области изменения функций, в него входящих, упрощает поиски корней.

Пример 3. Решить уравнение

Рассмотрим функции, стоящие в левой и правой частях уравнения, . Найдем их множество значений . Воспользуемся утверждением 1: так как множества значений имеет общую точку 2, от уравнения можно перейти к системе 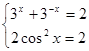. Решением системы, а, значит, и исходного уравнения является .

Утверждение 4. Пусть дано неравенство . Если множества значений этих функций имеют общую точку; , то неравенство равносильно системе .

Пример 4. Решить неравенство .

ОДЗ неравенства есть все действительные x, кроме -1. Разобьем ОДЗ на три промежутка и рассмотрим неравенство на каждом из этих промежутков. На первом и третьем промежутках неравенство выполняется для любого x: (); (); (). Следовательно, оба промежутка являются решением неравенства. На втором промежутке , то есть неравенство решений не имеет. Исходя из этого получаем решением неравенства .

Постановка домашнего задания.

1) Выучить теоретический материал.

2) Найти множество значений функций:

а); б) .

3) Решить уравнение .

Занятие №6 Тема: «Использование понятия области изменения функции при решении уравнений».

Цель: закрепить знания по теме «Использование понятия области изменения функции при решении уравнений».

Ход занятия:

Проверка домашнего задания. До начала занятия один из учеников записывает домашнее задание на доске учитель и другие ученики проверяют решение.

Решение задач. На доске написан список задач. Учащиеся по одному решают у доски. Учитель напоминает, что данные уравнения и неравенства решаются с использованием множества значений функций, в них входящих.

;

;

;

;

;

;

;

;

;

.

Подведение итогов занятия.

Учитель выставляет баллы за занятие: 1 балл за решение домашнего задания, по одному баллу за решение задач у доски

Главные разделы

• Главная
• Методы обучения двигательным действиям
• Раннее обучение английскому языку
• Педагогика способностей
• Половое воспитание детей и подростков
• Я-концепция ребенка дошкольного возраста
• Коррекция гиперактивных детей
• Информация о педагогике