Разработка занятий элективного курса

;

.

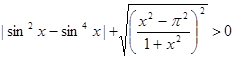Вариант 2.

;

; Пожарная сигнализация цена по материалам http://tornado.spb.ru.

.

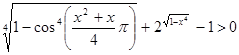Подведение итогов занятия. Учитель выставляет баллы полученные учениками. 1 балл ставится ученику, объяснявшему домашнее задание.

Постановка домашнего задания

Решите уравнения и неравенство:

;

;

;

.

Занятие №8 Тема: «Использование свойств четности или нечетности и периодичности функций».

Цель: знакомство с новым приемом решения уравнений и неравенств – использование свойств четности, нечетности и периодичности функций.

Ход занятия:

Проверка домашнего задания. До начала занятия двое учащихся выписывают решение на доске. Остальные на занятии проверяют правильность решения.

Актуализация знаний.

‑Какие функции называются четными, какие нечетными?

‑Приведите примеры.

‑Исследовать функции на четность: ;.

‑Сформулируйте определение периодической функции.

‑Какие из перечисленных функций являются периодическими, укажите их период: , , .

Изучение нового материала.

Утверждение 1. Пусть дана функция с областью существования X. Пусть дано число α ≠0. Тогда функция имеет область существования X1, которая характеризуется свойством: для любого число , а для любого число . При этом, если функция имеет период T, то функция имеет период .

Утверждение 2. Если функция F(x) – периодическая, то решение уравнения F(x)=0 или неравенства F(x)>0 (F(x)<0) достаточно найти на промежутке, равном по длине периоду функции, после чего записать общее решение.

Утверждение 3. Чтобы решить уравнение F(x)=0, где F(x) – четная или нечетная функция, достаточно найти положительные (или отрицательные) корни, после чего записать отрицательные (или положительные) корни, симметричные полученным. Для нечетной функции корнем будет x=0, если это значение входит в область определения F(x). Для четной функции значение x=0 проверяется непосредственной подстановкой в уравнение.

Утверждение 4. Чтобы решить неравенство F(x)>0 (F(x)<0), где F(x) – четная функция, достаточно найти решения для x≥0 (или x≤0). Если решением данного неравенства является промежуток (x1, x2), где x1, x2 – числа одного знака или одно из них равно нулю, то его решением будет и промежуток ( ‑ x2, ‑ x1).

Утверждение 5. Чтобы решить неравенство F(x)>0 (F(x)<0), F(x) – нечетная функция, достаточно найти его решения для x>0 (или x<0). Действительно, функция F(x) для любого x≥0 (x≤0) из области ее определения может находиться с нулем в одном из трех отношений: «равно», «больше», «меньше». Следовательно, если нам известно, при каких значениях x F(x)≥0 (F(x)≤0), то нам будет известно, при каких значениях x F(x)>0 (F(x)<0) (оставшиеся значения x из области определения). Но если нам известны промежутки знакопостоянства функции F(x) для x>0 (или x<0), то легко записать промежутки знакопостоянства и для x<0 (x>0).

Главные разделы

• Главная
• Методы обучения двигательным действиям
• Раннее обучение английскому языку
• Педагогика способностей
• Половое воспитание детей и подростков
• Я-концепция ребенка дошкольного возраста
• Коррекция гиперактивных детей
• Информация о педагогике