Использование свойств функций при решении уравнений и неравенств
Пример 2. Решить неравенство ![]()
Нахождение ОДЗ неравенства есть трудная задача, поэтому перейдем к равносильной ему системе неравенств![]()
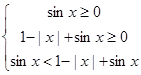 .
.
Третье неравенство имеет решение ![]() . Первое и второе неравенство справедливо лишь для x из промежутка
. Первое и второе неравенство справедливо лишь для x из промежутка ![]() . Поэтому этот промежуток является множеством решений системы.
. Поэтому этот промежуток является множеством решений системы.
Ответ: ![]() .
.
Использование монотонности функций при решении уравнений и неравенств. Это свойство при решении уравнений и неравенств используется чаще всего. Решение уравнений и неравенств с применением монотонности функций основывается на следующих утверждениях:
2.1Пусть f(x) – непрерывная и строго монотонная функция на некотором промежутке. Тогда уравнение вида f(x)=c, где с – данная константа, может иметь не более одного решения на этом промежутке.
2.2.Пусть f(x) и φ(x) непрерывные на некотором промежутке функции. Тогда если f(x) монотонно возрастает, а φ(x) убывает, то уравнение f(x)=φ(x) имеет не более одного решения на этом промежутке.
2.3.Пусть функция f(x) возрастает на своей области определения. Тогда для решения неравенства f(x)>c достаточно решить уравнение f(x)=c. Если x0 – корень, то решениями неравенства будут значения ![]() , принадлежащие области определения f(x).
, принадлежащие области определения f(x).
Рассмотрим на примерах, как используются эти утверждения.
Пример 3. Решить неравенство ![]() . Существует стандартный прием решения: возведение в квадрат (при условии
. Существует стандартный прием решения: возведение в квадрат (при условии ![]()
![]() 0). Мы рассмотрим решение данного неравенства с использованием свойства монотонности. Функция, расположенная в левой части неравенства, монотонно возрастает, в правой части - убывает. Из этого следует, что уравнение
0). Мы рассмотрим решение данного неравенства с использованием свойства монотонности. Функция, расположенная в левой части неравенства, монотонно возрастает, в правой части - убывает. Из этого следует, что уравнение ![]() имеет не более одного решения, причем если x0 – решение этого уравнения, то при
имеет не более одного решения, причем если x0 – решение этого уравнения, то при ![]() будет
будет ![]() , а решением данного неравенства будет
, а решением данного неравенства будет ![]() . Значение
. Значение ![]() легко подбирается:
легко подбирается: ![]() .
.
Ответ: ![]() .
.
Пример 4. Решить уравнение ![]()
Данное уравнение имеет очевидное решение ![]() . Докажем, что других решений нет. Поделим обе части на
. Докажем, что других решений нет. Поделим обе части на ![]() , получим
, получим ![]() . Левая часть представляет собой монотонно убывающую функцию. Правая часть функция постоянная. Следовательно, каждое свое значение она принимает один раз, то есть данное уравнение имеет единственное решение.
. Левая часть представляет собой монотонно убывающую функцию. Правая часть функция постоянная. Следовательно, каждое свое значение она принимает один раз, то есть данное уравнение имеет единственное решение.
Ответ: ![]() .
.
Уравнения вида ![]() . При решении уравнений данного вида используются следующие утверждения :
. При решении уравнений данного вида используются следующие утверждения :
пусть область существования функции ![]() есть промежуток M и пусть эта функция непрерывна и строго монотонна на этом промежутке. Тогда уравнение
есть промежуток M и пусть эта функция непрерывна и строго монотонна на этом промежутке. Тогда уравнение ![]() будет равносильно системе
будет равносильно системе 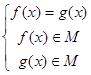 ;
;
Экспериментальное исследование уровня
сформированности социально-бытовых навыков в двух параллельных классах после
внедрения методики
При оценка уровня сформированности социально-бытовых навыков экспериментальной и контрольной групп нами было выделено три уровня социально-бытовых навыков:
1.Достаточный уровень;
2.Приближенный к достаточному уровень;
3.Недостаточный уровень.
Сравнительные данные о распределения учащихся по гр ...
Использование компьютерных средств обучения в образовании
На ранних стадиях развития человечества, когда обучение было непосредственно связано с трудовой деятельностью взрослого, дети не испытывали значительных затруднений, чтобы представить и понять то, чему их учили. С появлением письменности и книг обучение стало более сложным и трудным. Возникает про ...
Переход к третьему поколению Государственных Образовательных Стандартов
Современное образование в мире – самый массовый вид деятельности людей. В нём одновременно занято более миллиарда учащихся, в том числе более 85 млн. студентов, и почти 50 млн. педагогов. Образование становится главным делом жизни для подавляющего большинства людей молодого и среднего возраста, ко ...
Главные разделы
- Главная
- Методы обучения двигательным действиям
- Раннее обучение английскому языку
- Педагогика способностей
- Половое воспитание детей и подростков
- Я-концепция ребенка дошкольного возраста
- Коррекция гиперактивных детей
- Информация о педагогике
