Методические рекомендации к изучению темы "Логарифмические уравнения"

Цели: раскрыть понятие "логарифмическое уравнение"; ознакомить учащихся с основными приёмами и методами решения уравнений этого вида; обеспечить овладение всеми учащимися основными алгоритмическими приёмами решения логарифмических уравнений.

Урок 1 "Решение логарифмических уравнений".

Тему лучше изложить лекционно. Содержание лекции может быть следующим:

Простейшим логарифмическим уравнением (то есть уравнением, содержащим неизвестное под знаком логарифма) является , где , .

Логарифмическая функция возрастает (или убывает) на промежутке и принимает на этом промежутке все действительные значения. По теореме о корне: пусть функция возрастает (или убывает) на промежутке , число - любое из значений, принимаемых на этом промежутке. Тогда уравнение имеет единственный корень в промежутке . Отсюда следует, что для любого данное уравнение имеет и притом только одно решение. Из определения логарифма числа сразу следует, что является таким решением.

То есть если , , то корень уравнения равен .

Основной способ решения логарифмических уравнений - это потенцирование, в результате чего получаем обычное алгебраическое уравнение. Найденные корни необходимо проверить, так как возможны случаи появления посторонних корней.

При решении логарифмических уравнений и неравенств используйте свойства логарифмической функции. Для этого левую и правую части представляйте в виде логарифмов с одинаковыми основаниями. Необходимым шагом в решении является учёт области определения логарифмической функции.

Теорема: Уравнение , где , , равносильно системе:

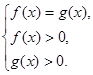
состоящей из уравнения и двух неравенств.

(В этой системе можно опустить одно из неравенств, так как каждое из них вытекает из уравнения и другого неравенства).

Таким образом для решения уравнения при , нужно:

1) решить уравнение f (x) =g (x);

2) из найденных корней отобрать те, которые удовлетворяют неравенству f (x) >0 (или, то же самое, неравенству g (x) >0; обычно используют более простое из этих неравенств), а остальные корни отбросить, так как они являются для данного уравнения посторонними.

Итак, логарифмическим называется уравнение, содержащее неизвестную величину под знаком логарифма.

Выделяют следующие основные методы решения логарифмических уравнений:

На основании определения логарифма.

Так решаются уравнения вида .

Приведём пример такого уравнения и решим его.

Пример: Решить уравнение .

Решение: ОДЗ: .

По определению логарифма имеем: (по формуле ).

Отсюда:

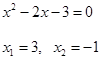
Проверка: - верно.

- верно.

Ответ:

Метод потенцирования.

Суть метода заключается в следующем: с помощью формул уравнение привести к виду . Это уравнение (при , ) равносильно системе

Главные разделы

• Главная
• Методы обучения двигательным действиям
• Раннее обучение английскому языку
• Педагогика способностей
• Половое воспитание детей и подростков
• Я-концепция ребенка дошкольного возраста
• Коррекция гиперактивных детей
• Информация о педагогике