Методические рекомендации к изучению темы "Логарифмические уравнения"
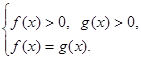
Пример: Решить уравнение 
.
Решение:
ОДЗ: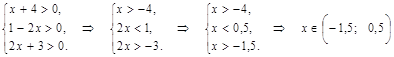 
Перенесём из правой части в левую: 
, а из левой в правую: 
, получим:
Применим свойства логарифмов:
; 
.
Проверка:
1) 
, 
- корень.
2) 
- не существует.
Ответ: .
Метод подстановки.
Обычную замену (подстановку) производят после некоторых преобразований
Пример: Решить уравнение 
.
Решение:
ОДЗ: 
Используя формулы, запишем уравнение так:
, то есть 
.
Заменяем 
. Тогда 
, то есть 
.
Отсюда 
,
.
Поэтому 
и 
.
Отсюда 
и 
Сделав проверку можно убедиться, что оба корня - корни данного уравнения.
Ответ: 
, .
Метод приведения к одному основанию.
Обычно условие примера подсказывает, к какому основанию следует перейти. Используются формулы:
.
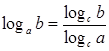
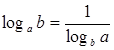
Как правило, метод приведения к одному основанию "работает" с методом подстановки.
Пример:
Решить уравнение 
.
Решение:
ОДЗ: 
, перейдём к основанию 2:
, то есть
.
Обозначим 
. Тогда 
, то есть
,
.
Значит, 
.
Ответ: 
.
Метод логарифмирования.
Обычно логарифмируют уравнения вида 
. Поясним этот метод на примере.
Пример: Решить уравнение 
.
Решение:
Область допустимых значений переменной x дана в условии задания.
Логарифмируем по основанию 10:
, то есть
.
Обозначим 
. Тогда 
, то есть
Психологические основы
При разработке уроков следует обратить внимание на основные психические процессы человека, потому, как и общедидактические принципы обучения, и основные методы обучения основываются на психических процессах человека.
Различают следующие психические процессы:
- ощущение;
- восприятие;
- внимани ...
Проекты по реорганизации народного образования, созданные во время буржуазной французской революции
В 70—80-х годах XVIII века во Франции создалась революционная ситуация.
В недрах феодального общества выросли и созрели формы нового, капиталистического уклада. Однако феодально-абсолютистский режим задерживал развитие капитализма, сельского хозяйства, промышленности и торговли. Французская буржу ...
Современные этапы экономики специального образования в России
За счет государственных именных образовательных финансовых обязательств производится оплата затрат на создание специальных условий для получения образования лицами с ограниченными возможностями здоровья, обеспечение указанных лиц учебниками, учебными пособиями, индивидуальными техническими средств ...
Главные разделы
- Главная
- Методы обучения двигательным действиям
- Раннее обучение английскому языку
- Педагогика способностей
- Половое воспитание детей и подростков
- Я-концепция ребенка дошкольного возраста
- Коррекция гиперактивных детей
- Информация о педагогике