Вид домашних упражнений направленных на развитие творческих качеств учащихся
1. Задачи на построение, решаемые любыми или указанными методами. Многие конструктивные задачи можно решить несколькими способами. Поэтому время от времени следует предлагать учащимся рассмотрению задачи снова решить произвольно выбранным из указанном методом. Эти упражнения могут иметь следующий вид:
ü решить задачу, уже решенную в классе:
a) тем же методом, но изменив ход решения;
b) любым другим методом;
c) указанным методом;
ü предложить решить задачу:
a) двумя, тремя любыми способами;
b) двумя, тремя указанными способами.
2. Составление учащимся задач на построение.
Может потребовать, чтобы составляемая учащимися задача удовлетворяла одному из следующих условий:
a) была бы аналогичной данной задачи на построении;
b) решалась бы указанным способом;
c) требовала бы применения двух (трех) данных геометрических мест
d) при решении которой применялась указанная теорема, например Пифагора или деления отрезка в данном отношении.
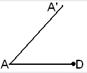
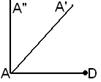
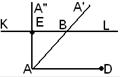
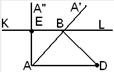
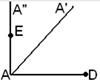
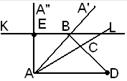
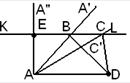
3. Изготовление таблицы, иллюстрирующей постепенное выполнение требуемого построения. Такой вид домашних упражнений имеет целью закрепить в памяти учащихся не только сами операции построения, но последовательность их выполнения. Существенность таких упражнений заключается в том, чтобы учащиеся сами изготовили таблицу, которая бы пояснила чертежами решение рассмотренной задачи, причем в строгой последовательности. Так, на первом чертеже изображается первая операция построения, на втором – вторая и т.д. Например. Построить трапецию ABCD, если даны основание (AD=a), угол при оснований (
), высота трапеции (h) и угол между диагоналями (
). Дать таблицу чертежей, показывающих последовательные решения
|
AD=a
На прямой Прямая KL такая, что KL ║AD, E KL пересекает Соединив точки B и D отрезком прямой, получим диагональ BD. Из точки А проводим такую прямую Прямая Соединив, точки C и D отрезком прямой и получим искомую трапецию. |
|
- луч такой, что 
- луч такой, что 
, 
и 
лежат по одну сторону от AD.
от точки А отложим отрезок АЕ, равный данной высоте h трапеции.
KL.
в точке В
, которая образует с диагональю BD угол 
Эстетическое воспитание ребенка средствами компьютерной графики
Ребенок входит в жизнь распахнутый к принятию красоты. Мамин голос, руки, глаза, слова прекрасны для всех и навсегда. Это точка отсчета. Начало всех начал. Отсюда ведут пути к светлой радости открытия красоты; к способности видеть, ценить и творить прекрасное.
Казалось бы, в эстетической области ...
Программа Е.Н. Лебеденко "Развитие самосознания
и индивидуальности"
Программа "Какой Я?". Развитие самосознания и индивидуальности.
Цель программы направлена на развитие самосознания и индивидуальности, эмоциональной сферы и индивидуальных способностей, коммуникативных навыков и социальной активности. Автор предлагает программу, которая предназначена дл ...
Цели и задачи обучения творческим
работам слабослышащих школьников
Учитель и ученик должны сотрудничать под единым девизом: «Знать – уметь – творить – хотеть совершенствоваться и реализовываться».
Каждый ребенок по-своему талантлив, но ему нужно помочь найти себя, раскрыть свои способности, реализоваться. И я как педагог всегда ставлю перед собой цель – увидеть, ...
Главные разделы
- Главная
- Методы обучения двигательным действиям
- Раннее обучение английскому языку
- Педагогика способностей
- Половое воспитание детей и подростков
- Я-концепция ребенка дошкольного возраста
- Коррекция гиперактивных детей
- Информация о педагогике