Приемы устных вычислений, основанные на законах и свойствах арифметических действий

2‑й случай.

2) (если из какого-либо числа вычесть и затем прибавить одно и то же число, то данное число не изменится) (первый случай переместительности членов ряда сложений и вычитаний) (если к какому-либо числу прибавить и затем вычесть одно и то же число, то данное число не изменится) . Итак, .

2. Прибавление разности к числу (первый случай сочетательности членов ряда сложений и вычитаний).

(если к какому-нибудь числу прибавить и затем вычесть одно и то же число, то данное число не изменится) (сочетательный закон) (производим сложение и вычитание). Итак, .

При решении подобных примеров применяется следующее правило: чтобы к числу прибавить разность, достаточно прибавить к нему уменьшаемое и из полученной суммы вычесть вычитаемое.

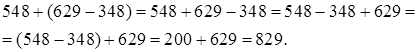
В этом случае правило может быть сформулировано так: чтобы к числу прибавить разность, достаточно из данного числа вычесть вычитаемое и к полученному числу прибавить уменьшаемое.

3. Вычитание из числа суммы (второй случай сочетательности членов ряда сложений и вычитаний).

(если из какого-нибудь числа вычесть и затем прибавить одно и то же число, то данное число не изменится) (на том же основании) = (переместительный и сочетательный законы) (если к какому-нибудь числу прибавить и затем вычесть одно и то же число, то данное число не изменится) . Итак, .

Чтобы из числа вычесть сумму, достаточно вычесть из него одно за другим каждое слагаемое.

4. Вычитание из числа разности (третий случай сочетательности членов ряда сложений и вычитаний).

1) (если из какого-нибудь числа вычесть и затем прибавить одно и то же число, то данное число останется без изменения) (на том же основании) (переместительность членов ряда сложений и вычитаний) (сочетательность членов ряда сложений и вычитаний) (если к какому-нибудь числу прибавить и затем вычесть одно и то же число, то данное число не изменится) = . Итак, .

Чтобы из числа вычесть разность, достаточно вычесть уменьшаемое и затем прибавить вычитаемое.

2) (вычитание из числа разности) (переместительность членов ряда сложений и вычитаний) (сочетательность суммы) (выполняем сложение и вычитание полученных чисел).

Таким образом, чтобы из числа вычесть разность, достаточно прибавить к нему вычитаемое и затем отнять уменьшаемое. Так как в математике нельзя из меньшего числа вычитать большее, то в случае, когда уменьшаемое больше числа, из которого вычитается разность, применить можно лишь второе из этих правил. Во всех остальных случаях выбираем то правило вычитания из числа разности, которое дает более быстрые и простые вычисления.

Главные разделы

• Главная
• Методы обучения двигательным действиям
• Раннее обучение английскому языку
• Педагогика способностей
• Половое воспитание детей и подростков
• Я-концепция ребенка дошкольного возраста
• Коррекция гиперактивных детей
• Информация о педагогике