Система домашних упражнений
Обстоятельное решение более менее сложной геометрической задачи на построение требует много времени. Между тем на уроки геометрии в средней школе отводиться сравнительно мало часов. В силу этих причин учитель математики решает весьма огромное количество задач на построение, а остальные упражнения этого рода предлагаются учащимся порядке домашнего задания, причем, если есть в этом необходимость, дает соответствующие пояснения и указания.
Рассмотрим виды домашних упражнений, которые можно предложить учащимся.
Пропедевтический вид домашних упражнений для решения конкретных задач
1. Простейшие графические построения.
В стабильном учебнике основные задачи на построение излагаются после того, как учащиеся пройдут смежные и вертикальные углы, свойства сторон треугольника, признаки равенства треугольников, ознакомятся с некоторым геометрическим местом точек. Между тем учащиеся с первых же дней знакомства с геометрией должны выполнять некоторые простейшие построения, чтобы в дальнейшем при решении геометрических задач на построение не встречать затруднений в выполнении графической стороны таких упражнений. Причем, учащимся разрешается использоваться не только циркулем и линейкой, но и транспортиром, и чертежным угольником.
2. Построить угол (без транспортира)
![]()
плоскость ![]() , если известно, что
, если известно, что
![]()
![]() .
.
3. Построение отрезков, определенных алгебраическими формулами.
4. Установление связи между данными геометрическими образами.
Эти упражнения побуждают учащихся вдумываться в условие предлагаемой задачи, развивают в них умение отыскивать те метрические закономерности между данным геометрическими образами, с изменением которых изменяется конфигурация этих образов.
5. Определение возможных конфигураций данных геометрических образов. Эти упражнения приучают вдумчиво относиться к условию задачи. Особенно желательно, чтобы в каждом отдельном случае выполнение такого упражнения предшествовало решению задачи, в которой имеют место рассматриваемые конфигурации геометрических образов. Вот некоторые из таких упражнений:
1) указать возможные конфигурации следующих геометрических образов: … .
2) сколько точек касания и пересечения и при каких конфигурациях могут иметь следующие геометрические образы
3) пояснить чертежами в каких случаях окружность и правильный пятиугольник могут иметь 8, 9, 10 общих точек,
4) дать различные конфигурации трех окружностей.
Задача: Пояснить чертежами, при каких конфигурациях и сколько общих точек имеют контуры треугольника и четырехугольника.
a. Одна общая точка
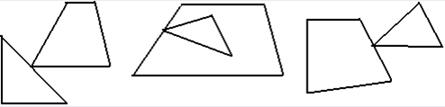
b. Две общие точки
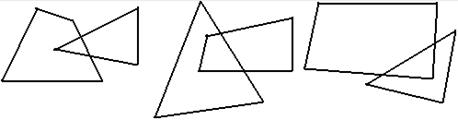
c. Три общие точки
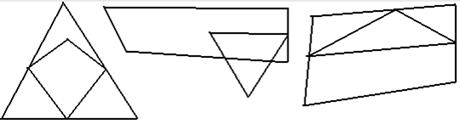
d. Четыре общи точки
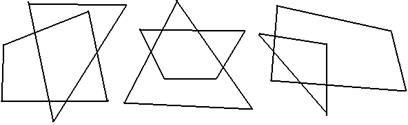
e. Пять общих точек
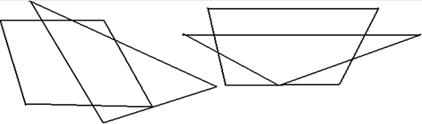
f. Шесть общих точек
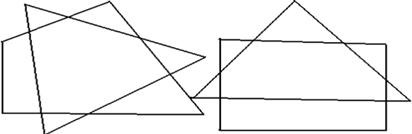
g. Бесконечно много общих точек
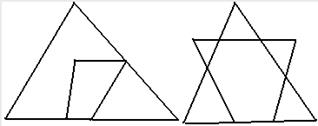
Естественнонаучные основы развития психомоторных функций
Изучение психомоторного развития человека в его многоуровневых и многогранных проявлениях определяется местом психомоторной организации в целостной психологической структуре человека как индивида, личности, субъекта важнейших социальных видов деятельности — труда, познания, общения.
Двигательные ...
Проблемы, возникающие во время обучения и пути их решения
Как любое нововведение, методика инновационного обучения имеет свои трудности, возникающие при внедрении её в классическую педагогику. Прежде всего, сложности возникают из-за личностных особенностей учащихся и педагогов. Методика, разработанная Элькониным- Давыдовым предполагает тесное сотрудничес ...
Содержание, формы и методы нравственного воспитания
по Я.А. Коменскому
"Управление человека собой является, по мнению Коменского, одной из трех целей воспитания. Оно достигается нравственным воспитанием."
Необходимо отметить, что точка зрения Коменского на школьное нравственное образование отличается от ныне общепринятой в России. Здесь для сокращения ра ...
Главные разделы
- Главная
- Методы обучения двигательным действиям
- Раннее обучение английскому языку
- Педагогика способностей
- Половое воспитание детей и подростков
- Я-концепция ребенка дошкольного возраста
- Коррекция гиперактивных детей
- Информация о педагогике
