Сравнительный анализ содержания школьных учебников по теме

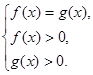
состоящей из уравнения и двух неравенств.

Даётся краткий алгоритм для решения логарифмических уравнений:

Для решения уравнения при , нужно:

1) решить уравнение f (x) =g (x);

2) из найденных корней отобрать те, которые удовлетворяют неравенству f (x) >0 (или, то же самое, неравенству g (x) >0; обычно используют более простое из этих неравенств), а остальные корни отбросить, так как они являются для данного уравнения посторонними.

Далее рассматриваются примеры решения логарифмических уравнений, но в данном учебнике они более сложные.

В учебнике А.Г. Мордковича тема "Логарифмические уравнения" выделена отдельным пунктом. Понятие логарифмического уравнения дано следующим образом:

"Логарифмическими уравнениями называют уравнения вида

,

где a - положительное число, отличное от 1, и уравнения, водящиеся к этому".

Сформулирована теорема:

Если и , то логарифмическое уравнение (где , ) равносильно уравнению .

Выделяются три основных метода решения логарифмических уравнений:

1) Функционально-графический метод. Он основан на использовании графических иллюстраций или каких-либо свойств функции (он был рассмотрен ранее при изучении свойств функции).

2) Метод потенцирования. Он основан на теореме, изложенной в параграфе.

3) Метод введения новой переменной.

Все методы решения логарифмических уравнений рассмотрены в данном параграфе на примерах, или в предыдущих параграфах.

Задачный материал включает: простейшие логарифмические уравнения, а также более сложные, содержащие в подлогарифмическом выражении квадратный трёхчлен и иррациональность, содержащие в основании дробные числа, выражения с переменной и иррациональность, дробные логарифмические уравнения, уравнения, содержащие логарифм в степени, логарифмические неравенства и системы уравнений. В учебниках Колмогорова и Мордковича выделены обязательные задания и задания повышенного уровня. Профильное различие заключается в количестве практического материала и в сложности предлагаемых заданий.

Сравнительный анализ содержания школьных учебников показал, на наш взгляд, что для работы в классе с углубленным изучением математики, т.е. для физико-математических классов, больше всего подходит учебник Н.Я. Виленкина, для общеобразовательных классов учебники С.М. Никольского и А.Г. Мордковича, для гуманитарных классов, в которых математика изучается по минимуму учебник А.Н. Колмогорова.

Специально разработанные учебники по математике для разных профилей на данный момент ещё не получили широкого распространения, поэтому при подготовке к уроку учитель пользуется несколькими учебниками и различными методическими пособиями. Например, при подготовке к уроку математики в классе физико-математического профиля некоторые учителя пользуются одновременно учебниками А.Г. Мордковича и Н.Я. Виленкина, что обусловлено полнотой содержания по данной теме и трудностью подобранного задачного материала. В этом состоит одна из проблем обучения математике в классах разного профиля.

§ 4. Модульная карта изучения темы "Логарифмические уравнения"

Главные разделы

• Главная
• Методы обучения двигательным действиям
• Раннее обучение английскому языку
• Педагогика способностей
• Половое воспитание детей и подростков
• Я-концепция ребенка дошкольного возраста
• Коррекция гиперактивных детей
• Информация о педагогике