Математические задачи, решаемые при помощи движений

Самостоятельные работы данного типа приводят школьников «к осмысленному переносу знаний в типовые ситуации, учат анализировать условие задачи, формируют приемы и методы познавательной деятельности, способствуют развитию внутренних мотивов к познанию, создают условия для развития мыслительной активности школьников. Реконструктивно-вариативные работы формируют основания для дальнейшей творческой деятельности ученика.

Самостоятельные работы эвристического типа данного вида формируют умения и навыки поиска ответа за пределами известного образца. Ученик сам определяет путь решения задачи и находит его. Значительный интерес вызывает у учащихся решение задач на построение фигур. С большим интересом учащиеся решают задачи на построение соответственных точек и самостоятельно могут предложить различные способы построения. Наличие нескольких способов решения этих задач будут вызывать повышенную активность учащихся. В этом и будет состоять часть эвристической самостоятельной работы.

Поиску различных вариантов решения способствуют лабораторные работы, а также задачи следующего вида:

Отрезки АВ и A1B1 симметричны относительно прямой р. Построить точку, симметричную точку К, К принадлежит АВ относительно оси р.

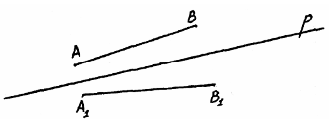
Учащиеся могут предложить такие варианты решения данной задачи:

1) через точку провести прямую, перпендикулярную прямой s. Точка пересечения этой прямой с отрезком А1B1 является искомой;

2) на отрезке A1B1 от точки А1 отложить отрезок А1К1 равный отрезку АК. Точка К1 является искомой.

Самостоятельные работы целесообразно предлагать всем учащимся, независимо от их интересов. Разный уровень заданий будет проявляться в формулировании условия для каждой группы учащихся.

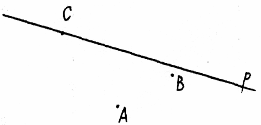
1. Постройте точки А’ и B’ симметричные данным точкам А и В относительно оси р. Постройте точку, симметричную точке С.

1. Постройте отрезки A’B’, A’C’ и B’С’ симметричные данным отрезкам АВ, АС и ВС относительно оси p. Воспользуйтесь предыдущей задачей.

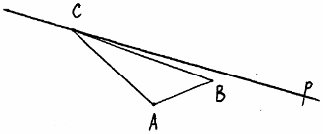
3. Постройте фигуру. F’ симметричную F относительно оси р. Отметьте две точки на сторонах данной фигуры, соедините их и постройте отрезок, симметричный данному относительно оси p.

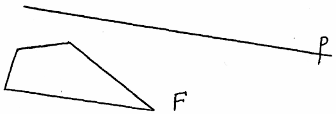
Творческие самостоятельные работы являются венцом системы самостоятельной деятельности школьников, которая позволяет учащимся получать принципиально новые для них знания, закрепляет навыки самостоятельного поиска знаний. Задачи такого типа - одно из самых эффективных средств формирования творчески развитой личности.

Для развития навыков творческой самостоятельности в применении геометрических преобразований 1-2 раза в учебном году учащимся можно предложить написать домашнее сочинение по данной теме. Темы сочинений целесообразно предложить непосредственно при изучении геометрических преобразований. Данная работа будет способствовать осмыслению школьниками темы и ее своевременному повторению.

Главные разделы

• Главная
• Методы обучения двигательным действиям
• Раннее обучение английскому языку
• Педагогика способностей
• Половое воспитание детей и подростков
• Я-концепция ребенка дошкольного возраста
• Коррекция гиперактивных детей
• Информация о педагогике