Фрагмент урока для 11-го класса по теме «Иррациональные уравнения»
Мы рассмотрели один из способов решения иррациональных уравнений. Это возведение обеих частей уравнения в квадрат. А если переменная находится под знаком корня 3-ей, 4-ой и т.д. степени. Тогда как быть?
(Предполагаемый ответ: возвести обе части уравнения в 3-ю, 4-ю и т.д. степень).
Учитель: Кто попытается сформулировать общий способ решения иррациональных уравнений?
Выслушать все высказывания и в завершении подвести итог.
Учитель: «Значит одним из способов решения иррациональных уравнений является возведение обеих частей уравнения в степень, равную показателю степени корня. И не забыть, при этом сделать проверку, отсеяв, возможные посторонние корни».
Закрепление изученного материала – 10 мин.
Учитель: Итак, существует несколько способов решения иррациональных уравнений. Мы сегодня рассмотрели только некоторые из них. Давайте, перечислим, какие это способы?
(Предполагаемый ответ: возведение обеих частей уравнения в степень, равную показателю степени корня, графический способ, способ замены переменной).
Учитель: Расскажите алгоритм решения уравнений каждого из способов.
Учащиеся очень быстро проговаривают три алгоритма.
Учитель: Молодцы! А теперь прошу внимание на плакат
Плакат с уравнениями:
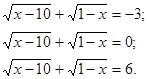
Рис. 9
Учитель: Как решить первое уравнение?
Выслушивает все варианты ответов. Если будут затруднения, вспоминает еще раз с учащимися определение арифметического квадратного корня и обратить внимание на доску с карточками, 
, где записаны условия выполнения равенства
(Ответ: уравнение не имеет решения).
Второе уравнение. Учащиеся дают свои варианты решения. Учитель их внимательно выслушивает, корректирует, задает наводящие вопросы, если это необходимо. И все вместе делают вывод, что уравнение не имеет корней.
Третье уравнение. Все необходимые рассуждения высвечиваются на экран. Решаем это уравнение с помощью области определения уравнения. В итоге получаем систему:
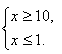
которая не имеет решений. Следовательно, и уравнение не имеет решений.
Плакат с решением уравнений:
|
Решение уравнений:
 
    |
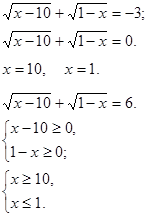Рис. 10
Фрагмент урока для 8-го класса по теме «Квадратный корень из произведения»
Комментарии к уроку
Данный урок является уроком изучения нового материала по теме «Квадратный корень из произведения». Его основная цель - вывести формулу квадратного корня из произведения и сформировать опыт в выполнении исследовательских заданий.
Урок разработан таким образом, что учащиеся, пу ...
Методические особенности изучения темы «Треугольники и четырехугольники»
Основная задача образования – создание личностью целостной картины мира, и, соответственно, процесс обучения, ориентированный на развитие личности, должен обеспечивать ребенка такими знаниями и в такой организации, чтобы он мог на их основе постепенно формировать целостное представление о мире.
У ...
Методика обучения ходьбе на лыжах в старшем дошкольном возрасте
Обучение детей дошкольного возраста ходьбе на лыжах обязательно начинается с подготовительного периода. Подготовительный период охватывает сентябрь, октябрь, ноябрь, то есть те месяцы, когда снежный покров для передвижения на лыжах еще не достаточен. На прогулке с детьми, одетыми в облегченную оде ...
Главные разделы
- Главная
- Методы обучения двигательным действиям
- Раннее обучение английскому языку
- Педагогика способностей
- Половое воспитание детей и подростков
- Я-концепция ребенка дошкольного возраста
- Коррекция гиперактивных детей
- Информация о педагогике